Notes:
Bootstrapping follows the idea of pooling, but studies the uncertainty in the frequency estimate obtained by repeatedly resampling the data.
Ex.: Consider a data set has, say, 60 persons. The number of occurrences of A and B is known for each person. Researchers now form a so-called ‘bootstrap sample’ with 60 data points. This means, that random persons from the original data set are taken with replacement. Thus, the same person can occur several times in the bootstrap sample. Then, the frequency of A is computed by using pooling (e.g. 12.571). This is repeated for 1,000 (different) bootstrap samples, and the variation in the frequencies of A tells about the uncertainty in the original estimate of the frequency of A.
Output carried out by this method is a confidence interval.
To calculate a mean using bootstrapping, you proceed the same way as in ‚Pooling‘.
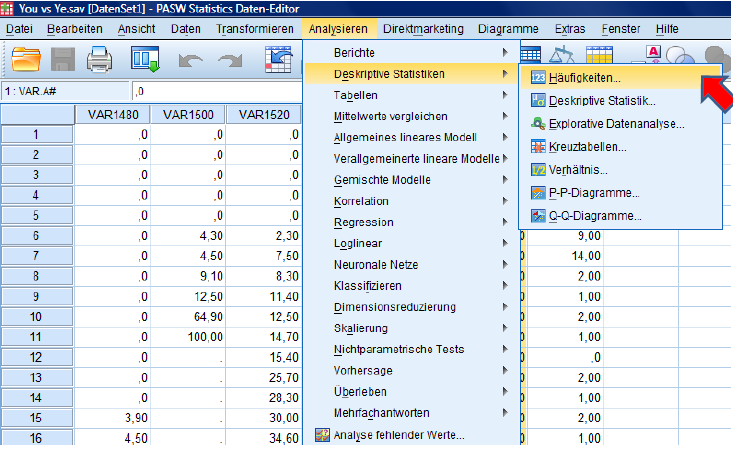
Go to ‚Analyze‘ … ‚Descriptive Statistics‘ … ‚Frequencies‘
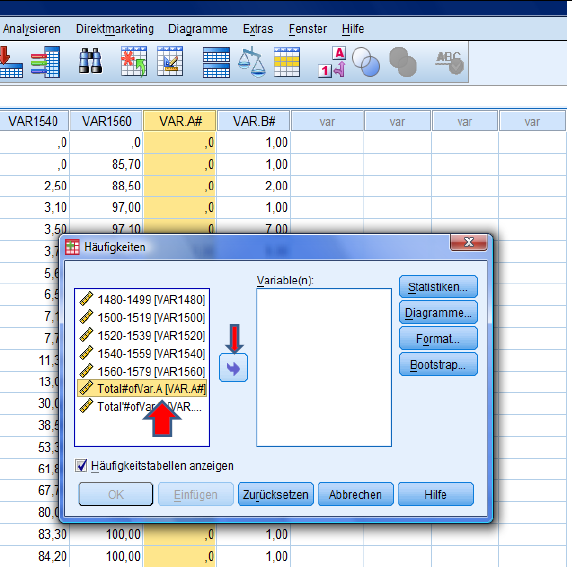
Activate column 6 by marking it in the left table and then clicking on the arrow.
It should then appear in the right box (‚Variables‘).
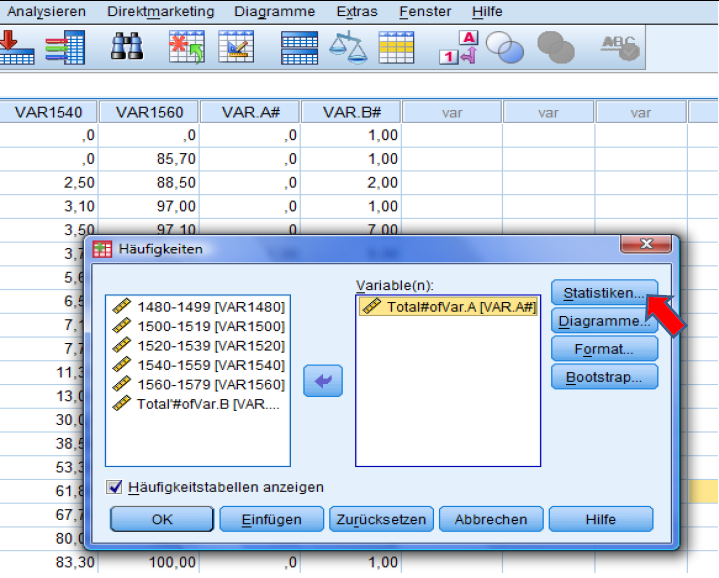
Now, click on ‚Statistics‘
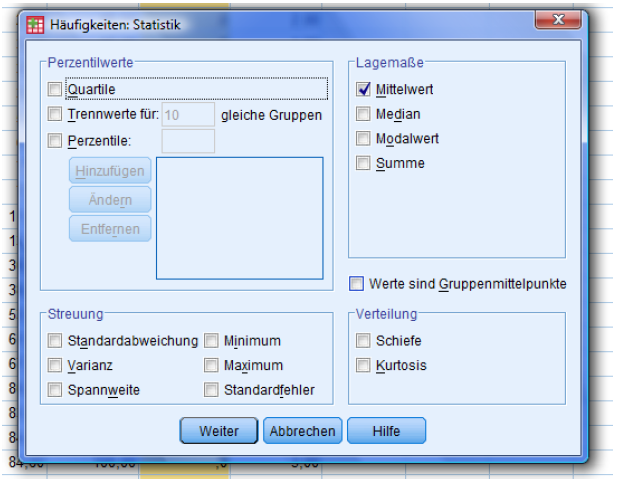
The only option you need, is to activate the mean.
Press continue.
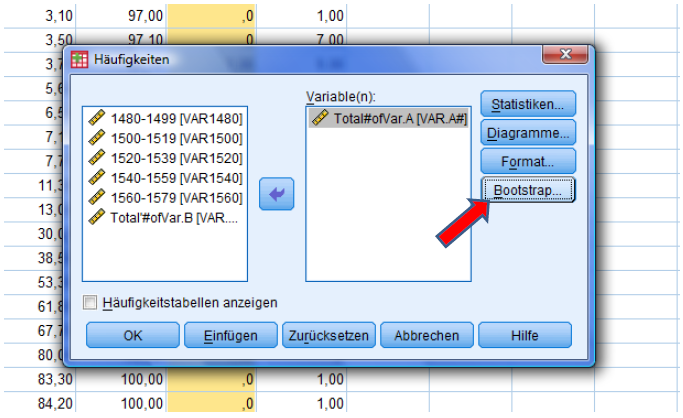
Then you need to select ‚Bootstrap…‘.
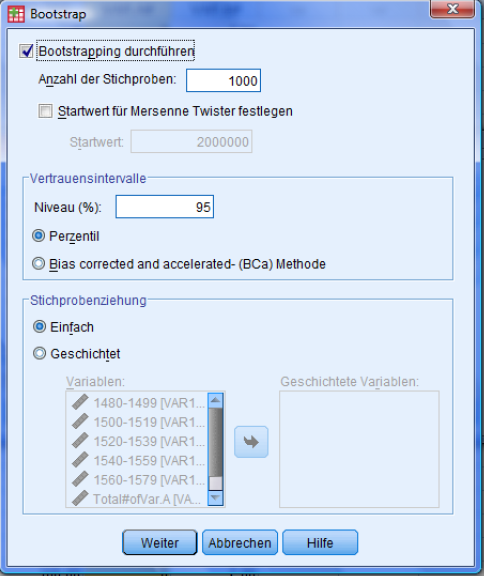
The only task is to select: Conduct bootstrapping.
The other settings should be left untouched, since they are a standard setting which does not need to be changed.
Click on continue and then OK.

Your Bootstrap output features:
Interpretation:
A 95% confidence interval of 0.3023 – 0.7674 means that with a large number of repeated samples, 95% of the calculated confidence intervals would include the true (but unknown) value of the parameter.
Created with the Personal Edition of HelpNDoc: Full-featured EPub generator