5 Sample size

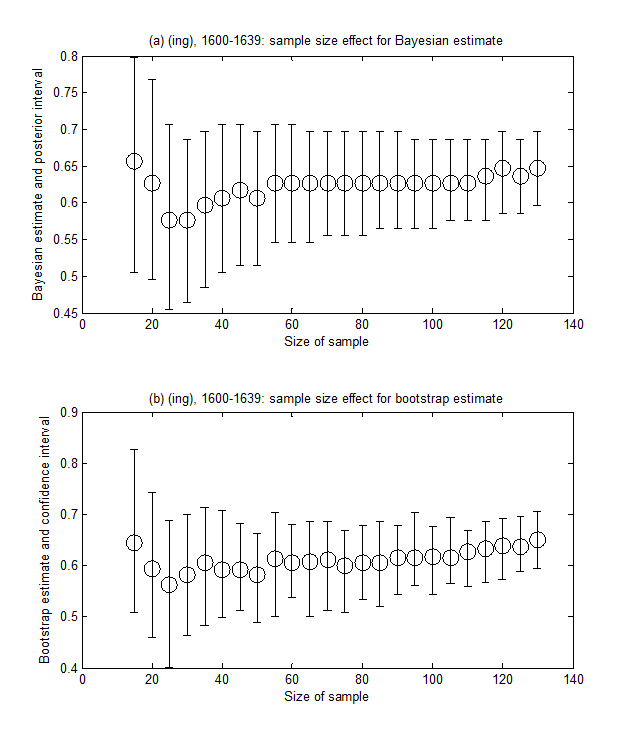
Different sample sizes are likely to have different effects on estimates. This is also an issue that is addressed by Mannila et al. and therefore shall briefly be touched upon here, as well. The representativeness of a particular sample in regards to, for instance, the use of a linguistic variable within a community is always dependent on its size. In general, the larger the sample, the more likely it is that one's answers will truly reflect the population, as a larger sample allows for the true value to be averaged out. This raises the question of how large a sample must at least be in order to yield realistic results. In this regard, the aforementioned Bayesian methods or bootstrap techniques provide much insight as they indicate posterior or confidence intervals (also called margin of error). The confidence interval, for instance, specifies a range within in which the true (average) value can be located. Small samples yield large intervals, thus giving less accurate estimates, while larger samples give more precise estimates. Interestingly enough, Mannila et al. have discovered that, for some applications, a sample of size 30 is likely to yield fairly reliable results, with the width of its interval varying only slightly from the interval width of samples of sizes 50 and above.

Also, an issue that needs to be considered and which is also addressed by Mannila et al. is that the informants on which a sample is based individually contribute differing amounts of data. This leads to the question of which effect informants contributing only small amounts of data may have on the results. In this regard, Mannila et al. demonstrate that the results of their case study as described in Chapter 18 are hardly affected by informants that have contributed less than 10 occurrences of a linguistic variable. Therefore, in general, one should always aim to include only informants that have contributed a certain amount of data in one's sample.

Created with the Personal Edition of HelpNDoc: Produce Kindle eBooks easily